Utility - Wikipedia, the free encyclopedia. In economics, utility is a measure of preferences over some set of goods and services. The concept is an important underpinning of rational choice theory. Utility is an important concept in economics and game theory, because it represents satisfaction experienced by the consumer of a good. A good is something that satisfies human wants. Since one cannot directly measure benefit, satisfaction or happiness from a good or service, economists instead have devised ways of representing and measuring utility in terms of economic choices that can be measured. Economists have attempted to perfect highly abstract methods of comparing utilities by observing and calculating economic choices. In the simplest sense, economists consider utility to be revealed in people's willingness to pay different amounts for different goods. Applications[edit]Utility is usually applied by economists in such constructs as the indifference curve, which plot the combination of commodities that an individual or a society would accept to maintain a given level of satisfaction. Utility and indifference curves are used by economists to understand the underpinnings of demand curves, which are half of the supply and demand analysis that is used to analyze the workings of goods markets. Individual utility and social utility can be construed as the value of a utility function and a social welfare function respectively. When coupled with production or commodity constraints, under some assumptions these functions can be used to analyze Pareto efficiency, such as illustrated by Edgeworth boxes in contract curves. Such efficiency is a central concept in welfare economics. In finance, utility is applied to generate an individual's price for an asset called the indifference price. Utility functions are also related to risk measures, with the most common example being the entropic risk measure. Revealed preference[edit]It was recognized that utility could not be measured or observed directly, so instead economists devised a way to infer underlying relative utilities from observed choice. These 'revealed preferences', as they were named by Paul Samuelson, were revealed e. Utility is taken to be correlative to Desire or Want. It has been already argued that desires cannot be measured directly, but only indirectly, by the outward phenomena to which they give rise: and that in those cases with which economics is chiefly concerned the measure is found in the price which a person is willing to pay for the fulfillment or satisfaction of his desire.[1]: 7. Utility functions[edit]There has been some controversy over the question whether the utility of a commodity can be measured or not. At one time, it was assumed that the consumer was able to say exactly how much utility he got from the commodity. The economists who made this assumption belonged to the 'cardinalist school' of economics. Today utility functions, expressing utility as a function of the amounts of the various goods consumed, are treated as either cardinal or ordinal, depending on whether they are or are not interpreted as providing more information than simply the rank ordering of preferences over bundles of goods, such as information on the strength of preferences. Cardinal utility[edit]When cardinal utility is used, the magnitude of utility differences is treated as an ethically or behaviorally significant quantity. For example, suppose a cup of orange juice has utility of 1. With cardinal utility, it can be concluded that the cup of orange juice is better than the cup of tea by exactly the same amount by which the cup of tea is better than the cup of water. One cannot conclude, however, that the cup of tea is two thirds as good as the cup of juice, because this conclusion would depend not only on magnitudes of utility differences, but also on the "zero" of utility. 
Neoclassical economics has largely retreated from using cardinal utility functions as the basis of economic behavior. A notable exception is in the context of analyzing choice under conditions of risk (see below). Sometimes cardinal utility is used to aggregate utilities across persons, to create a social welfare function. The argument against this is that interpersonal comparisons of utility are meaningless because there is no simple way to interpret how different people value consumption bundles.[citation needed]Ordinal utility[edit]When ordinal utilities are used, differences in utils (values taken on by the utility function) are treated as ethically or behaviorally meaningless: the utility index encodes a full behavioral ordering between members of a choice set, but tells nothing about the related strength of preferences. In the above example, it would only be possible to say that juice is preferred to tea to water, but no more. Ordinal utility functions are unique up to increasing monotone transformations. For example, if a function is taken as ordinal, it is equivalent to the function , because taking the 3rd power is an increasing monotone transformation. This means that the ordinal preference induced by these functions is the same. In contrast, cardinal utilities are unique only up to increasing linear transformations, so if is taken as cardinal, it is not equivalent to . Preferences and utility functions[edit]Although preferences are the conventional foundation of microeconomics, it is often convenient to represent preferences with a utility function and analyze human behavior indirectly with utility functions. Let X be the consumption set, the set of all mutually- exclusive baskets the consumer could conceivably consume. The consumer's utility function ranks each package in the consumption set. Utility Function Game Theory DefinitionIf the consumer strictly prefers x to y or is indifferent between them, then . For example, suppose a consumer's consumption set is X = {nothing, 1 apple,1 orange, 1 apple and 1 orange, 2 apples, 2 oranges}, and its utility function is u(nothing) = 0, u(1 apple) = 1, u(1 orange) = 2, u(1 apple and 1 orange) = 4, u(2 apples) = 2 and u(2 oranges) = 3. Then this consumer prefers 1 orange to 1 apple, but prefers one of each to 2 oranges. In micro- economic models, there are usually a finite set of L commodities, and a consumer may consume an arbitrary amount of each commodity. This gives a consumption set of , and each package is a vector containing the amounts of each commodity. In the previous example, we might say there are two commodities: apples and oranges. 
Game theory is the study of the ways in which interacting choices of economic agents produce outcomes with respect to the preferences (or utilities) of. In economics, utility is a measure of preferences over some set of goods and services. The concept is an important underpinning of rational choice theory. Explanation of risk, uncertainty, and certainty equivalents. Part of Mike Shor's lecture notes for a course in Game Theory. Game Theory. This article sketches the basic concepts of the theory of games in order to discuss some of their philosophical implications and problems. Economic and Game Theory What is Game Theory? by David K. Levine, Department of Economics, UCLA. top |general | research | classes | links | David 'You treat world. Game Theory 101: The Complete Textbook on Amazon: http:// http:// This lecture explains the Allais paradox. DEFINITION of 'Game Theory' A model of optimality taking into consideration not only benefits less costs, but also the interaction between participants. In decision theory, the von Neumann-Morgenstern utility theorem shows that, under certain axioms of rational behavior, a decision-maker faced with risky. 1. Introduction Using expected-utility theory, economists model risk aversion as arising solely because the utility function over wealth is concave. If we say apples is the first commodity, and oranges the second, then the consumption set and u(0, 0) = 0, u(1, 0) = 1, u(0, 1) = 2, u(1, 1) = 4, u(2, 0) = 2, u(0, 2) = 3 as before. Note that for u to be a utility function on X, it must be defined for every package in X. A utility function represents a preference relation on X iff for every , implies . If u represents , then this implies is complete and transitive, and hence rational. 
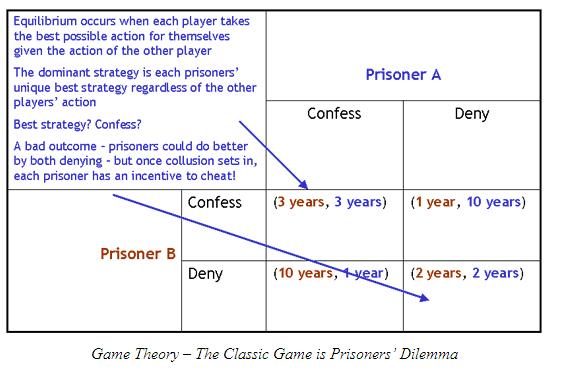
Examples of utility function forms[edit]In order to simplify calculations, various alternative assumptions have been made concerning details of human preferences, and these imply various alternative utility functions such as: Most utility functions used in modeling or theory are well- behaved. They are usually monotonic and quasi- concave. However, it is possible for preferences not to be representable by a utility function. An example is lexicographic preferences which are not continuous and cannot be represented by a continuous utility function.[3]Expected utility[edit]The expected utility theory deals with the analysis of choices among risky projects with (possibly multidimensional) outcomes. The St. Petersburg paradox was first proposed by Nicholas Bernoulli in 1. Daniel Bernoulli in 1. D. Bernoulli argued that the paradox could be resolved if decision- makers displayed risk aversion and argued for a logarithmic cardinal utility function. The first important use of the expected utility theory was that of John von Neumann and Oskar Morgenstern, who used the assumption of expected utility maximization in their formulation of game theory. Neumann–Morgenstern expected utility[edit]Von Neumann and Morgenstern addressed situations in which the outcomes of choices are not known with certainty, but have probabilities attached to them. A notation for a lottery is as follows: if options A and B have probability p and 1 − p in the lottery, we write it as a linear combination: More generally, for a lottery with many possible options: where . By making some reasonable assumptions about the way choices behave, von Neumann and Morgenstern showed that if an agent can choose between the lotteries, then this agent has a utility function such that the desirability of an arbitrary lottery can be calculated as a linear combination of the utilities of its parts, with the weights being their probabilities of occurring. This is called the expected utility theorem. The required assumptions are four axioms about the properties of the agent's preference relation over 'simple lotteries', which are lotteries with just two options. Writing to mean 'A is weakly preferred to B' ('A is preferred at least as much as B'), the axioms are: completeness: For any two simple lotteries and , either or (or both, in which case they are viewed as equally desirable). Archimedean property): If , then there is a between 0 and 1 such that the lottery is equally desirable as . Intuitively, if the lottery formed by the probabilistic combination of and is no more preferable than the lottery formed by the same probabilistic combination of and then and only then . Axioms 3 and 4 enable us to decide about the relative utilities of two assets or lotteries. In more formal language: A von Neumann–Morgenstern utility function is a function from choices to the real numbers: which assigns a real number to every outcome in a way that captures the agent's preferences over simple lotteries. What is Game Theory? What economists call game theory psychologists call the theory. Although game theory is relevant to parlor games such. There are two main branches of game theory. Noncooperative game theory. That is the branch of. I will discuss here. In addition to game theory, economic theory has three other. All are closely connected to game theory. The focus is on. preferences and the formation of beliefs. The most widely used form of. Probability theory is heavily used in order to represent the. Bayes Law is frequently used to model the. Decision theory. is often used in the form of decision analysis, which shows how best to. It is widely used in the macroeconomic analysis of broad. In recent years, political economy has emerged as a combination. Issues studied include tax policy, trade policy, and the role. European Union. differs from game theory in that game. Naturally this relies heavily on game theory. Questions addressed by. An. One way to describe a game is by listing the players (or. In the case of a two- player game, the actions of the first. The entries in the matrix are two numbers representing the. A very. famous game is the Prisoner's Dilemma game. In this game the two. Each suspect is placed in a separate cell, and offered the opportunity. The game can be represented by the following. Note that higher numbers are better (more utility). If neither. suspect confesses, they go free, and split the proceeds of their crime. However, if. one prisoner confesses and the other does not, the prisoner who. If both prisoners confess. This game has fascinated game theorists for a variety of. First, it is a simple representation of a variety of important. For example, instead of confess/not confess we could label. This captures a variety of situations economists describe as public. An example is the construction of a bridge. It is best. for everyone if the bridge is built, but best for each individual if. This is sometimes refered to in. Similarly this game could describe the. Naturally it is best for both firms if they both. A second feature of this game, is that it is self- evident how. No matter what a suspect. If. the partner in the other cell is not confessing, it is possible to get. If the partner in the other cell is confessing, it is. Yet the pursuit of individually. This conflict between the pursuit of individual goals and. A third feature of this game is that it changes in a very. Suppose for example that. In this case in the first period the suspects may reason. Strictly speaking, this conclusion is. However, repetition opens up. If. Some. of the power and meaning of game theory can be illustrated by assessing. If we were all better people the world would be a better. This may seem to you to be self- evidentally true. Or you may. recognize that as a matter of logic this involves the fallacy of. Game theory can give precise meaning to. In fact the statement is false, and. Prisoner's Dilemma. Let us start with a variation on the Prisoner's Dilemma game we may call the Pride Game. The Pride Game is like the Prisoner's Dilemma game with the addition of the new. A proud individual is one who will not confess. In. other words, if I stand proud and you confess, I get 1. I can stand proud before your humiliation, but you get 0, because you stand humiliated. On the other hand, if we are both proud, then neither. It would be worse. In this case, I would get 3. The Pride Game is very different than the Prisoner's. Dilemma game. Suppose that we are both proud. In the face of your. I simply chose not to confess I would lose face, and my. To confess would be even worse as. I would be humiliated as well. In other words, if we are both proud, and we each. Morever, as we are both correct, anything either of us learns will. This type of situation - . Nash Equilibrium. Notice. that the original equilibrium of the Prisoner's Dilemma confess- confess. Pride game: if I think you are going. I would prefer to stand proud and humiliate you rather than. Now. suppose that we become "better people." To give this precise meaning. Specifically, let us imagine that. I am more generous and care more about you, I place a value. I receive in the "selfish" game described above and. Not being completely altruistic, I. I do on yours. So, for. I get 3 units of utility, and you get. I am an altruist, I. I get 2/3 of the. Overall I get 4 units of utility instead of 3. Because I have. become a better more generous person, I am happy that you are getting 6. The new game with altruistic. This gives the payoff matrix of the Altruistic Pride Gameproudnot confessconfessproud. What. happens? If you are proud, I should choose not to confess: if I were to. I get a utility of 4, while if I choose not to confess I get. I do confess I get only 0. Looking at the. original game, it would be better for society at large if when you are. I were to choose not to confess. This avoids the confrontation of. However, as an. altruist, I recognize that the cost to me is small (I lose only. I prefer to "not confess." This is shown in. What should I do if you choose not to confess? If. am proud, I get 4. I choose not to confess I get 5, but if I. I get 5. 3. 3. So I should confess. Again, this is marked with an. Finally, if you confess, then I no longer wish to stand. If I choose not to confess I get only 0. So it. is best for me to. What do we conclude? It is no longer an. Each of us in the face of the. Of course it is. also not an equilibrium for us both to choose not to confess: each of. The only equilibrium is the box. So. far from making us better off, when we both become more altruist and. Notice how we can. If we both. receive a utility of 1 rather than both receiving a utility of 4, the. The key to game theory and to. It is true that if we. However: if we become more caring we will wish to. As this example shows, when we both try to do. To. put this in the context of day- to- day life: if we were all more. The behavior of criminals has a complication. More altruistic. criminals would choose to commit fewer crimes. However, as crime is not. If. in the balance more crimes are committed, the world could certainly be. The example shows how this might work. For. those of you who are interested in or already know more advanced game. Pride Game has only the one Nash equilibrium shown - it is. The Atruistic Pride Game, however, has. You can compute them using the fine. Gambit. written by Richard Mc. Kelvey, Andrew Mc. Lennan and Theodore Turocy. One. equilibrium involves randomizing between proud and confess, so is worse. Pride game. The other is. The. payoffs to that equilibrium gives each player 2. Pride Game. I'd. like to thank Jie Zheng for his help. The "We are all better people". Sung- Ha Hwang. and Samuel Bowles called "Is Altruism Bad For Cooperation?" If you know. I will provide a. They provide a much more. If you wish to learn more about game theory, there a variety.
0 Comments
Leave a Reply. |
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
September 2016
Categories |
 RSS Feed
RSS Feed
